MATLAB、Scilab、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その35【対称行列と二次形式⑦】
を書き直したもの。
正規方程式を導出するための対称行列と二次形式の話。
今回は二次形式の多項式表現と行列表現の計算をScilabで実施する。
ロードマップ【再掲】
ロードマップと今回使用する数式を再掲。

\(
x^TA\circ x^T
\begin{bmatrix}
1\\
\vdots\\
1
\end{bmatrix}
\)
計算する二次形式の数式
\(
3x^2+2y^2+5xy
\)
今回は、Scilabで実施する。
Scilabコード
Scilabコードは以下になる。
a=3;
b=2;
c=5;
A=[a c/2; c/2 b];
N=6;
ax=linspace(0,10,N);
ay=linspace(0,10,N);
[x,y]=meshgrid(ax,ay);
subplot(2,1,1);
polyY=a.*x.^2+b.*y.^2+c.*x.*y;
mesh(ax, ay, polyY);
X=[x(:)';y(:)'];
Y=X'*A.*X'*ones(2,1);;
matY=matrix(Y,N,N);
subplot(2,1,2);
mesh(ax, ay, matY);
polyY
matY
実行結果
実行結果は以下。
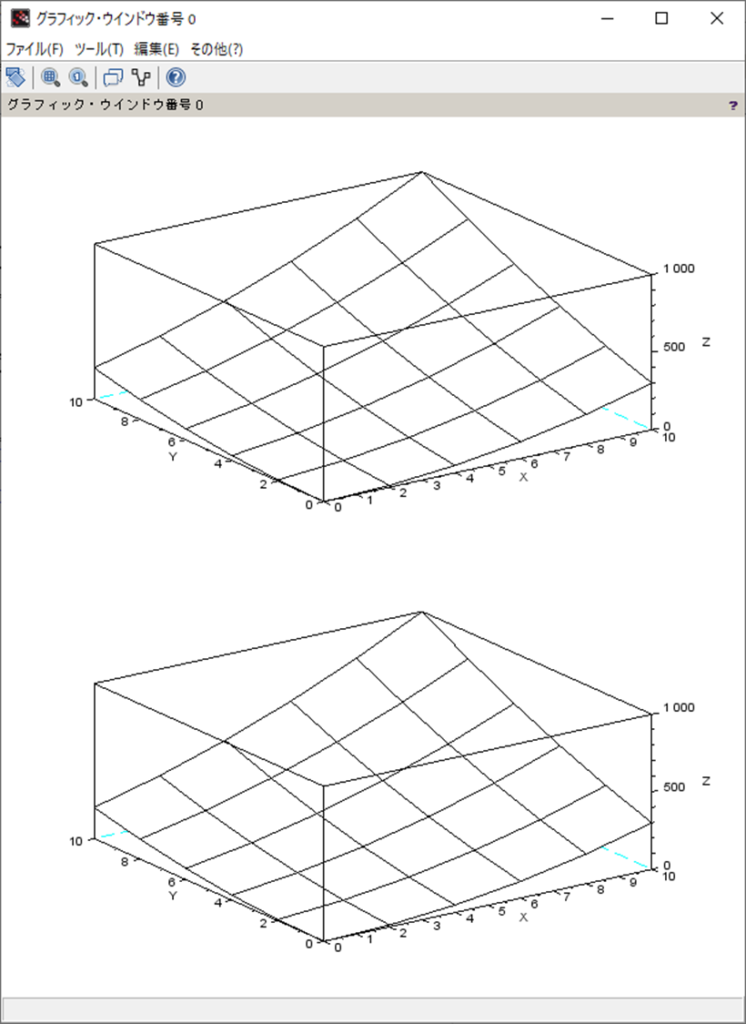
-->polyY
polyY =
0. 12. 48. 108. 192. 300.
8. 40. 96. 176. 280. 408.
32. 84. 160. 260. 384. 532.
72. 144. 240. 360. 504. 672.
128. 220. 336. 476. 640. 828.
200. 312. 448. 608. 792. 1000.
-->matY
matY =
0. 12. 48. 108. 192. 300.
8. 40. 96. 176. 280. 408.
32. 84. 160. 260. 384. 532.
72. 144. 240. 360. 504. 672.
128. 220. 336. 476. 640. 828.
200. 312. 448. 608. 792. 1000.
考察
ScilabはMATLABとほぼ同じになる。
二次形式の多項式表現、行列表現で同じ結果になった。
違うところというと、
行列の形状を変えるreshapeがmatrixになっているところ。
Scilabにはreshapeが無いので、類似機能のmatrixを使用している。
似てるけど、細かいところで差が出るのは仕方ない事なのだろう。
まとめ
- 二次形式の多項式表現と行列表現の計算をScilabで実施。
- 基本的にはMATLABと一緒。
- ただし、reshapeの代わりにmatrixを使う必要がある。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント