【入門】対称行列と二次形式【数値計算】

MATLAB、Scilab、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
ロードマップ【再掲】
対称行列
対称行列の性質
対称行列がどこで生きてくるのか？
二次形式
二次形式の一般化
次のページへ

はじめに

の、
MATLAB,Python,Scilab,Julia比較第2章その29【対称行列と二次形式①】
MATLAB,Python,Scilab,Julia比較第2章その30【対称行列と二次形式②】
MATLAB,Python,Scilab,Julia比較第2章その31【対称行列と二次形式③】
MATLAB,Python,Scilab,Julia比較第2章その32【対称行列と二次形式④】

を書き直したもの。

正規方程式を導出するための対称行列と二次形式の話。

ロードマップ【再掲】

正規方程式導出までのロードマップを再掲しておく。

対称行列

対称行列というものがある。
対称と言うと左右対称をイメージするかもしれないが、
対称行列は対角に対して対称な行列を指す。

3×3の正方行列で表現すると以下になる。

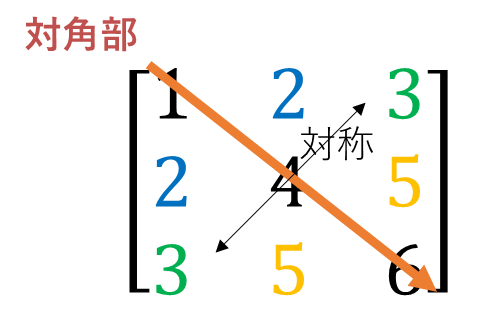
左上から右下へ斜め方向の要素を指して対角と呼ぶ。
あと、当然ではあるけど、必ず正方行列である。

ちなみに単位行列も対称行列に含まれる。
厳密には、対称行列の対角部以外が0になっているものを対角行列と呼び、
対角行列の対角部が全て1になっているものを単位行列と呼ぶ。

対称行列の性質

そして対称行列の性質を説明する。

これは当たり前と言えば当たり前なのだが、
転置しても値が変化しない。
以下を見るとわかると思う。

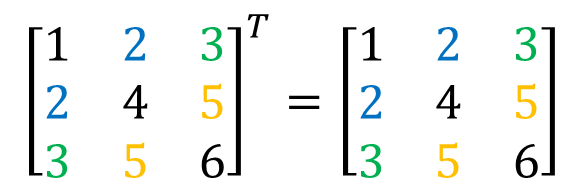
対称行列がどこで生きてくるのか？

この対称行列は、二次形式、二次形式の微分、グラム行列で使用する予定。
まずは対称行列というものの存在をしってもらうだけでOK。

二次形式

二次形式とはすべての項の次数が2である多項式のこと。
変数が\(x,y,z\)とあったとして以下な感じのものを指す。

\(
2x^2+y^2+z^2+xy+yz+xz
\)

各変数が自乗含めて2つまで掛ける項だけで構成されてる。

二次形式の一般化

そして、に二次形式を一般化すると以下になる。

\(
\displaystyle \sum_{i,j=1}^n a_{ij}x_i x_j
\)

そして、これをさらにベクトル、行列で表現すると以下になる。

\(
\begin{eqnarray}
\Bigg(
\begin{bmatrix}
a_{11} && a_{12} && \dots && a_{1n} \\
a_{21} && a_{22} && \dots && a_{2n} \\
\vdots && \vdots && \ddots && \vdots \\
a_{n1} && a_{n2} && \dots && a_{nn}
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{bmatrix}
\Bigg)^T
\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{bmatrix}\\=
\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{bmatrix}^T
\begin{bmatrix}
a_{11} && a_{12} && \dots && a_{1n} \\
a_{21} && a_{22} && \dots && a_{2n} \\
\vdots && \vdots && \ddots && \vdots \\
a_{n1} && a_{n2} && \dots && a_{nn}
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{bmatrix}
\end{eqnarray}
\)