【入門】最小二乗法(Scilab)【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
Scilabによる1次関数の最小二乗法
Scilabコード
実行結果
まとめ

はじめに

の、
MATLAB,Python,Scilab,Julia比較第2章その10【最小二乗法⑨】

を書き直したもの。

最小二乗法をScilabを使って解いてみる話。

Scilabによる1次関数の最小二乗法

Scilabは大体MATLABと似てること多いし、
PythonのNumpyも関数名はpolyfitだったから、きっとScilabも同じ。

と思いきや結構違う。

ここでは詳細説明は割愛するが、Scilabで使用する関数はlsq。
MATLAB、PythonのNumpyのpolyfitと比べると実は高機能。

難しい使い方もできるが、今回の1次関数を前提にした場合は、それほど難しくはない。
ただ、「なんでこんなパラメータなの？」という疑問は湧いてくるだろう。
これはもっと複雑な多項式にも適用できるためのものではある。

Scilabコード

Scilabコードは以下になる。

x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51]';
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40]';

A=[x,ones(x)];B=y; // 各項と結果
coef=lsq(A,B); // 最小二乗法で得られた1次関数の各係数
disp('各係数');
disp(coef);

plot(x,y,'+')
xp=linspace(0,4,400); // x軸
fx=coef(1)*xp+coef(2); // 2次関数
plot(xp,fx,'-k')
p=gca();p.tight_limits(:)="on";
p.data_bounds(:,2)=[10;41];
p.data_bounds(:,1)=[0;4];

実行結果

結果は以下になる。

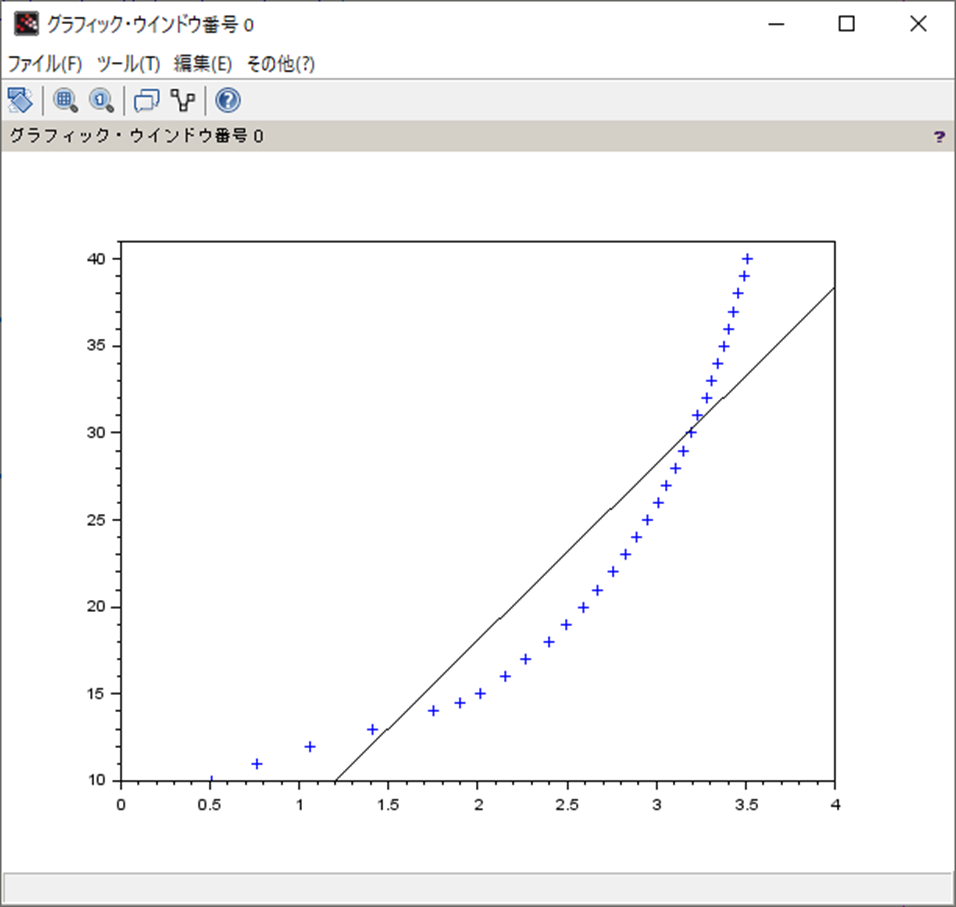
 各係数   
 
    10.133034  
  - 2.1616644

これも係数の値が微妙に違うが、表示精度の問題を加味すると同じ値と見なせる。

以下がScilabによる係数算出のところになる。

A=[x,ones(x)];B=y; // 各項と結果
coef=lsq(A,B); // 最小二乗法で得られた1次関数の各係数

Aに各項を入れる。
\(x^2\)のように二次の項を入れていけば、polyfitのような多項式に対する最小二乗法が実現できるし、
\(x\)以外の変数を入れると重回帰分析になる。
つまり、正規方程式のルールを適用できるということになる。

正規方程式については、追々説明する予定。

まとめ

Scilabによる1次関数の最小二乗法を実施。
- MATLABと一緒と思いきや、実はコンセプトレベルで違う。
- 正規方程式の仕様が丸見えになってるイメージ。
  - 正規方程式については追々説明していく予定。

MATLAB、Python、Scilab、Julia比較ページはこちら