バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
最小二乗法をPythonを使って解いてみる話。
(実際にはNumpy)
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
Pythonによる1次関数の最小二乗法

今回はPythonによる最小二乗法だね。

これもライブラリ使って一撃な感じ?

そうだね。
Numpyにpolyfitというメソッドが定義されていて、
使い方はMATLABのpolyfitと一緒だな。

おー!
同じ名称、同じ使い方ってのはありがたいねー!
(覚えるのが楽で)

しかし、今更だけど、polyfitってどういう意味になるの?

Polynomial fitの略のようだね。
Polynomialは日本語で多項式。
「多項式に合わせこむ」という意味合いのなるのだろう。
Numpyのマニュアルにも以下のように記載されてるしね。
Least squares polynomial fit.
Numpy reference(https://numpy.org/doc/stable/reference/generated/numpy.polyfit.html)

なるほど。
言葉の意味まで理解してるといろいろしっくり来るね。
Pythonコード

以下がPythonによる1次関数の最小二乗法を行うPythonコード
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51])
y = np.array([10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40])
coef = np.polyfit(x, y, 1) # 最小二乗法で得られた1次関数の各係数
print("各係数", end=':')
print(coef)
quad_func = np.poly1d(coef) # 1次関数の各係数から1次関数を生成
xp = np.linspace(0, 4, 400) # 同定した1次関数のx軸を生成
fx=coef[0]*xp+coef[1]; # 1次関数生成
plt.plot(x, y, '+', \
xp, fx, '-' )
plt.ylim(10,41)
plt.xlim(0,4)
plt.show()実行結果

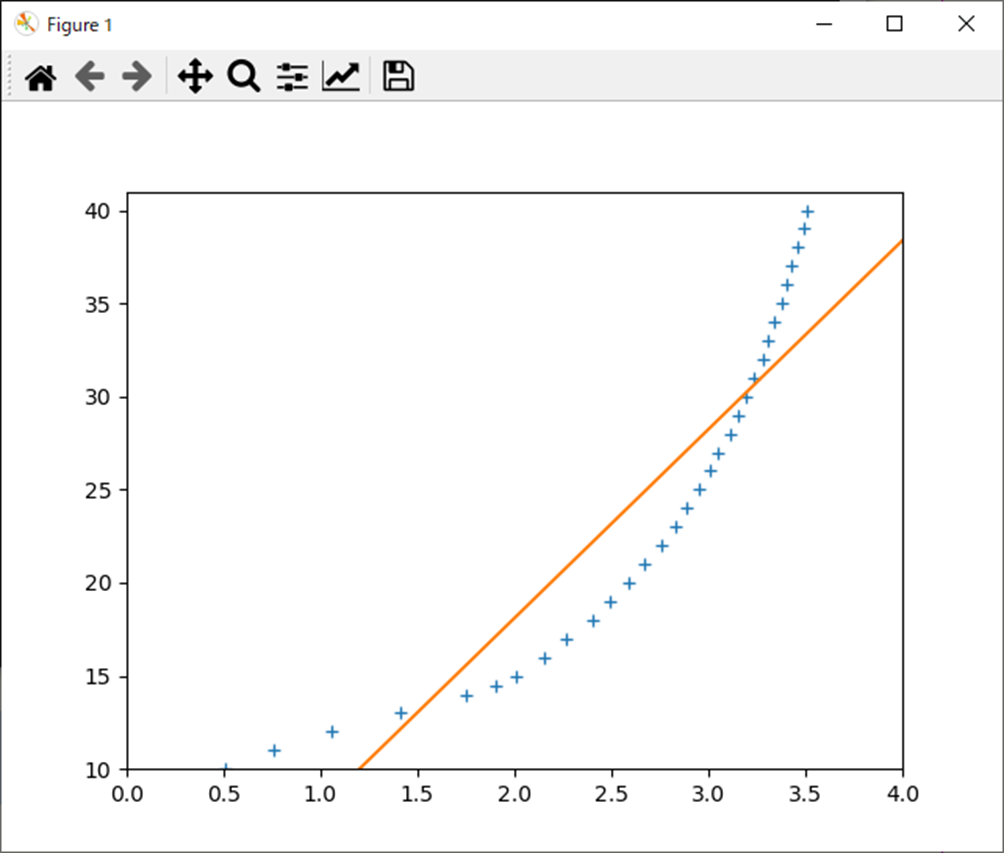
そして結果が以下。
各係数:
[10.13303351 -2.16166437]
線としては同じ感じになったね。

でも、係数の値がMATLABの時と違う?

おそらく表示精度の差だろう。
厳密には演算誤差の乗り方の差も含まれているだろうが、表示精度が支配的と思って良い。

つまり、同じ結果が得られたってことで良いってことか。

そうそう。
まとめ

まとめだよ。
- Pythonによる最小二乗法はNumpyのpolyfitで実施可能。
- 実際にコードを作成し、動作させてみた。
- ほぼ同一の係数が算出で来た。
- (表示精度の都合、見た目上は違う値にはなってる。)
バックナンバーはこちら。




コメント