バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
最小二乗法をMATLABを使って解いてみる話。
(polyfit関数を使う)
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
各ツールを使うと最小二乗法は一撃で解ける??

さて、前回までで最小二乗法についていろいろ説明したが・・・。

したが???

実は、MATLAB、Python、Scilab、Juliaを使うと一撃で解ける!!!

まじかーー!!
前回までの話はなんだったんだーー!!

まぁこのシリーズのコンセプトって
ベクトル、行列を駆使していろいろ解決しよう。
って感じじゃん?
各ツールのライブラリ的な機能を使うのは簡単だけど、
ライブラリを使わなかった、使えない状況とかもあり得て、
必要になる局面はあると思うよ。たぶん。
よって、ライブラリ未使用の方法もやる予定だ。

その言い方だと、ライブラリ的な機能を使うと一撃だけど、
前回の理屈を利用した方法でも同じように解けるからやってみる。
って感じなのかな??

そう解釈してもらってOKだ。
MATLABで最小二乗法

MATLABで最小二乗法を解く場合は、polyfitという関数を使うと、
\(x,y\)のプロットを元に、各次の係数が求まる。

マジかよ。
関数一個で解決すんのかよ。
x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
coef = polyfit(x, y, 1); % 最小二乗法で得られた1次関数の各係数
disp('各係数:');
disp(coef);
xp = linspace(0, 4, 400); % 同定した1次関数のx軸を生成
fx=coef(1)*xp+coef(2); % 1次関数生成
hold on
plot(x, y, '+',xp, fx, '-k' );
ylim([10,41]);
xlim([0,4]);実行結果

そして結果が以下になる。
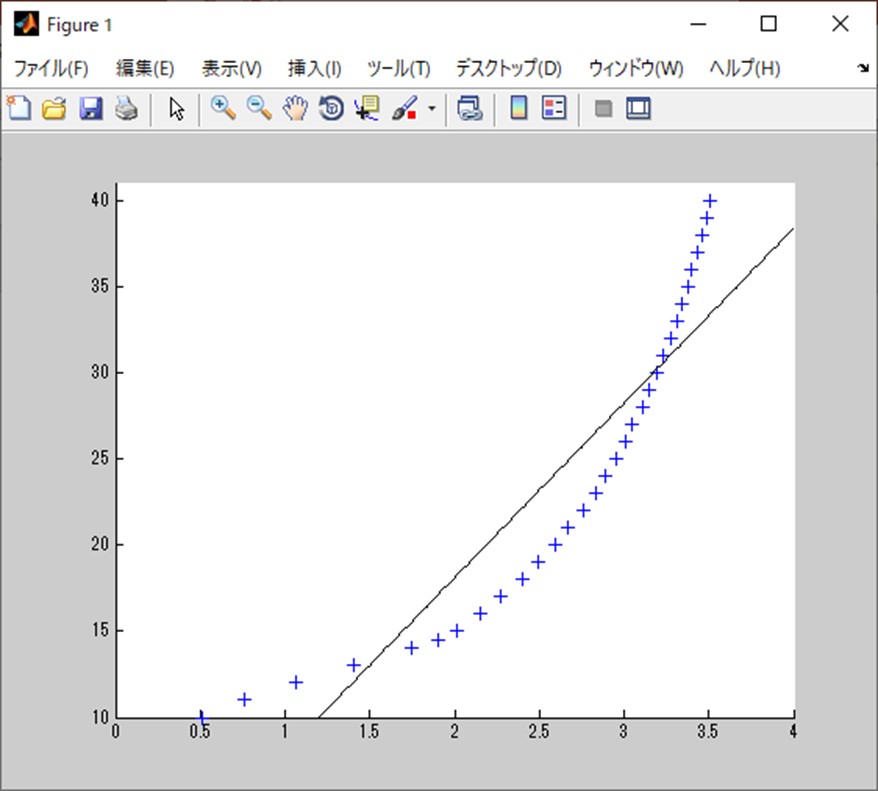
各係数:
10.1330 -2.1617
確かに、それっぽい線が引けてるね。

こんな感じで他の言語、ツールでもどうなるかを確認していく。
まとめ

まとめだよ。
- 各種ツール、言語を使うと最小二乗法が一撃で解ける。
- ライブラリ的な機能を使うことになる。
- 後日、ライブラリ未使用もやってみる予定。
- 今回はMATLABのpolyfitを使って最小二乗法を実施。
バックナンバーはこちら。




コメント