バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
まずは最もシンプルな回帰分析である、
1次関数の最小二乗法についての説明の続き。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
誤差関数の最小値を求めるには?

前回は、1次関数に於ける最小二乗法の誤差関数を求めた。
\(
\begin{eqnarray}
L(a,b)&=&\displaystyle\sum_{i=0}^n\{y_i -(ax_i +b)\}^2 \\
&=&\displaystyle a^2\sum x_i^2+nb^2+\sum y_i^2-2a\sum x_i y_i -2b\sum y_i +2ab\sum x_i
\end{eqnarray}
\)

で、誤差関数を最小化される\((a,b)\)を求める必要があると思うんだけど、
どうやって求めるの?総当たり?

まぁ、総当たりで求めるというのも一つの考え方だな。
求めたい一次関数於いて、\(a\)が傾き、\(b\)が切片なので、
適当にプロットした点に対して、それぞれを動かした場合の誤差関数\(L\)の値を見てみよう。
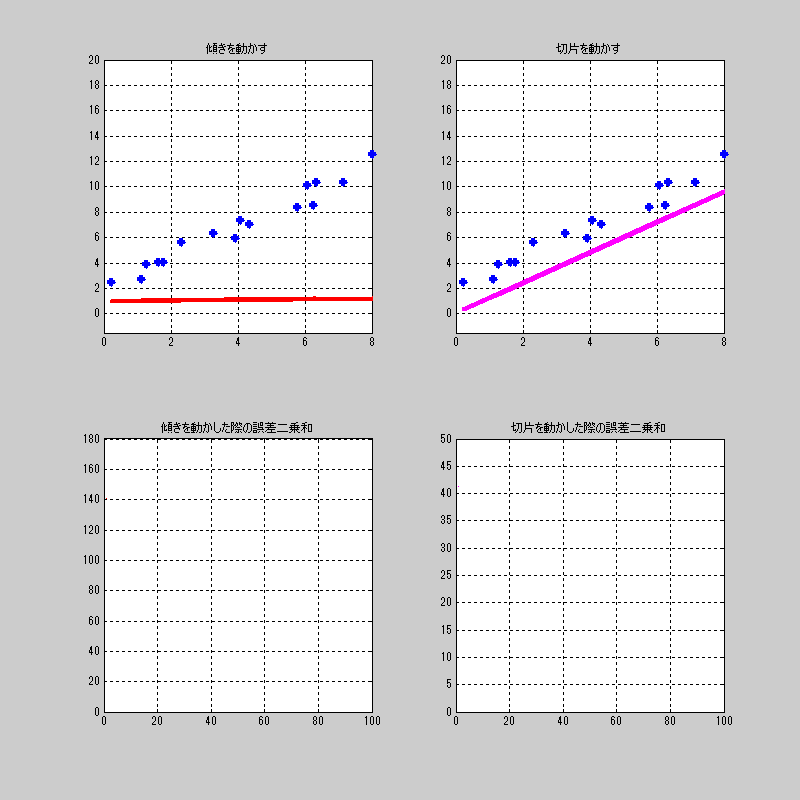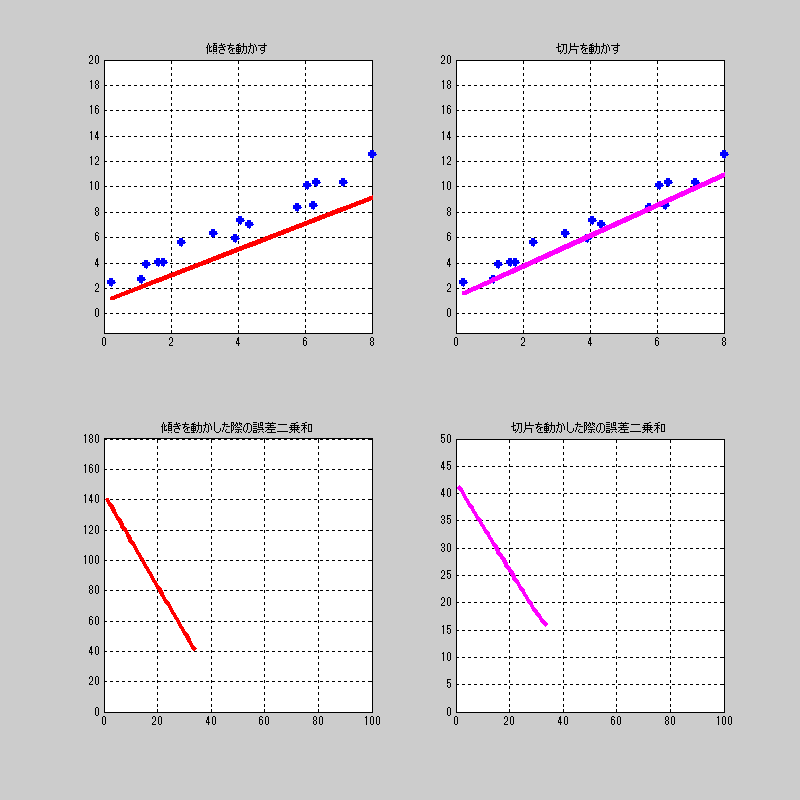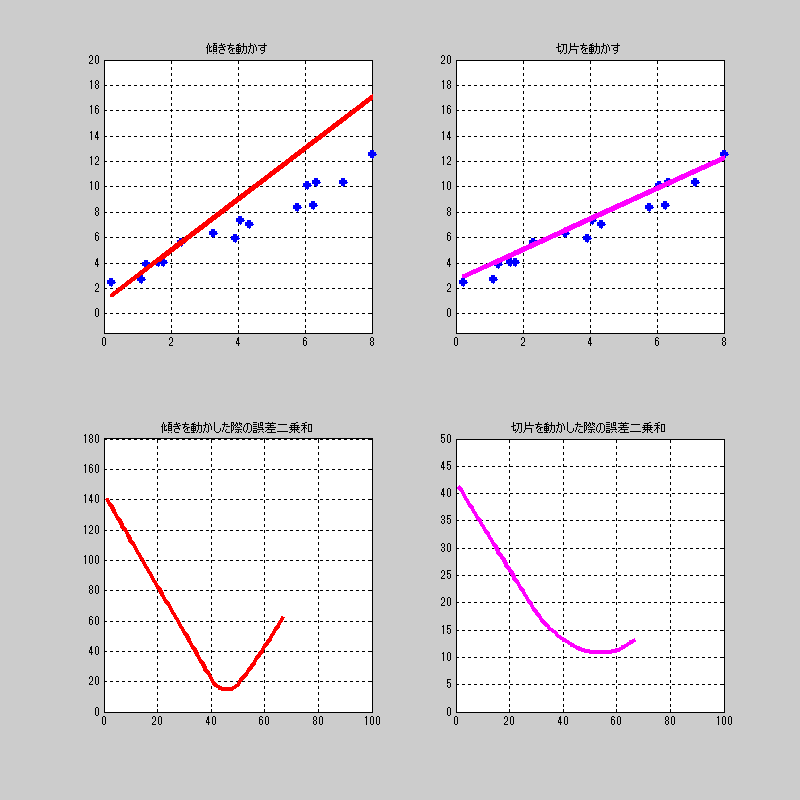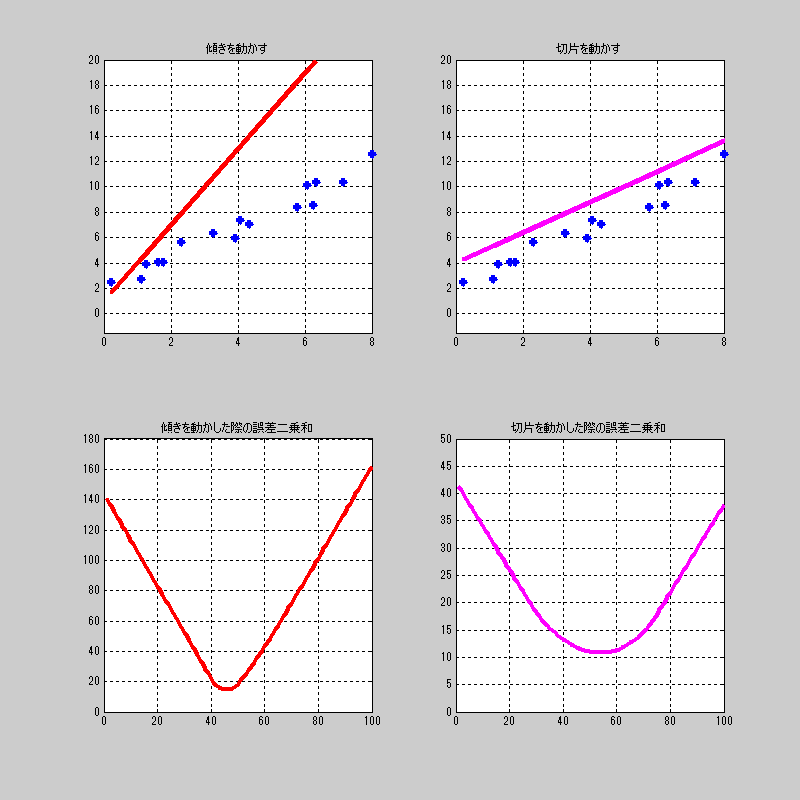

中々、おもしろい動きをするねー。
誤差関数を総当たりしてる雰囲気

先ほどの動画は、傾きだけを動かした場合、切片だけを動かした場合で、
実際の総当たりは、もっと大量の検査をすることになる。
ここでは切片をちょっと動かして、それに対して、傾きを総当たり。
を繰り返す画像を見せよう。
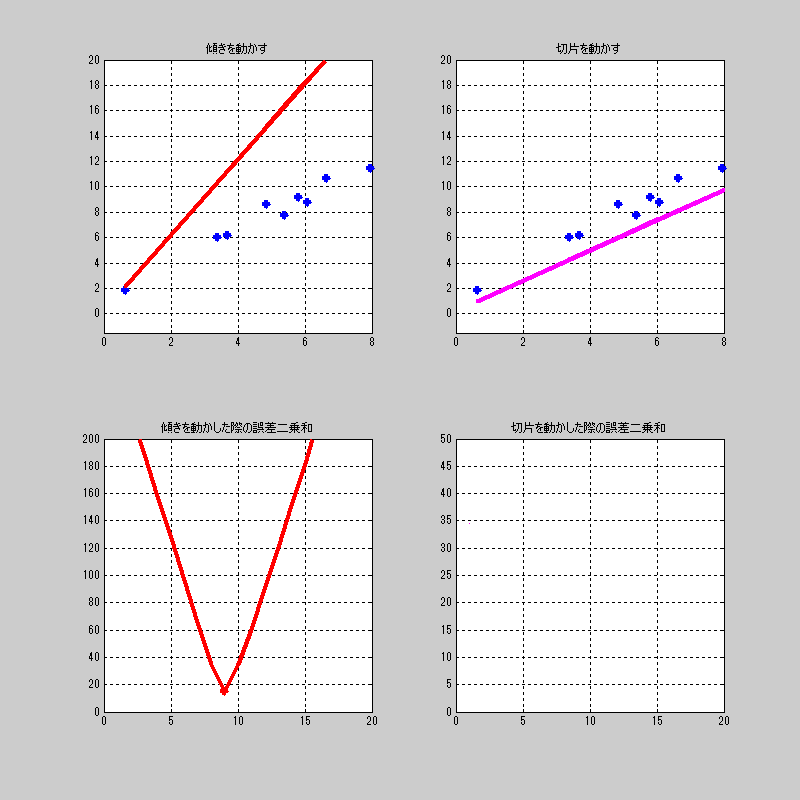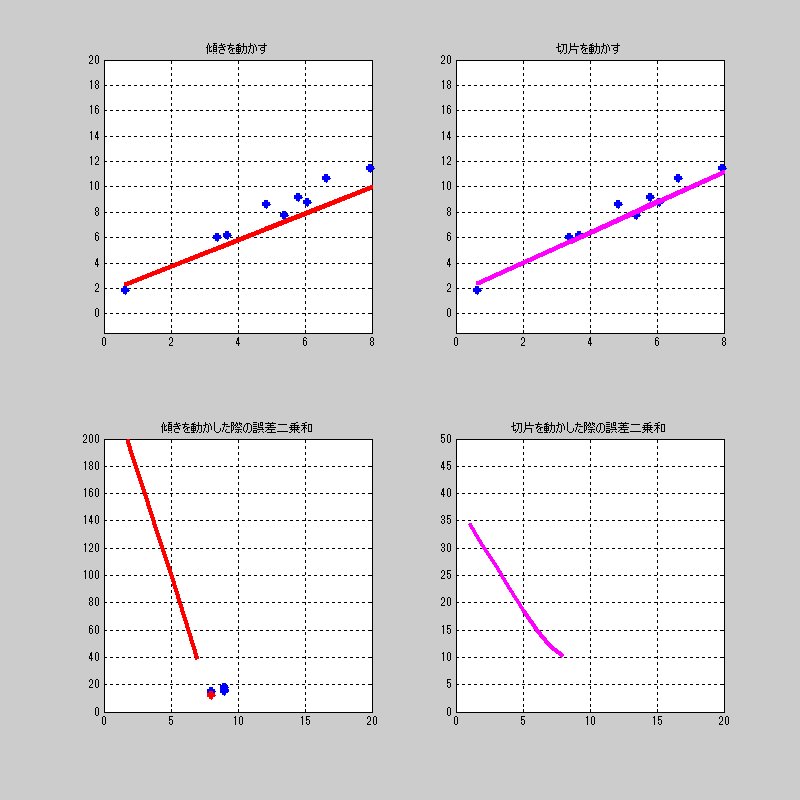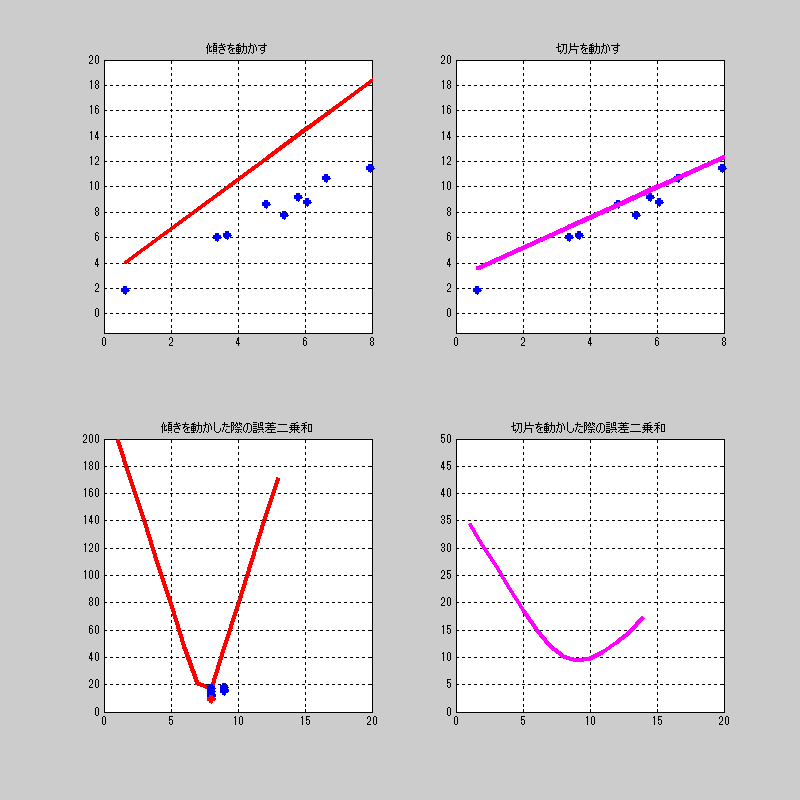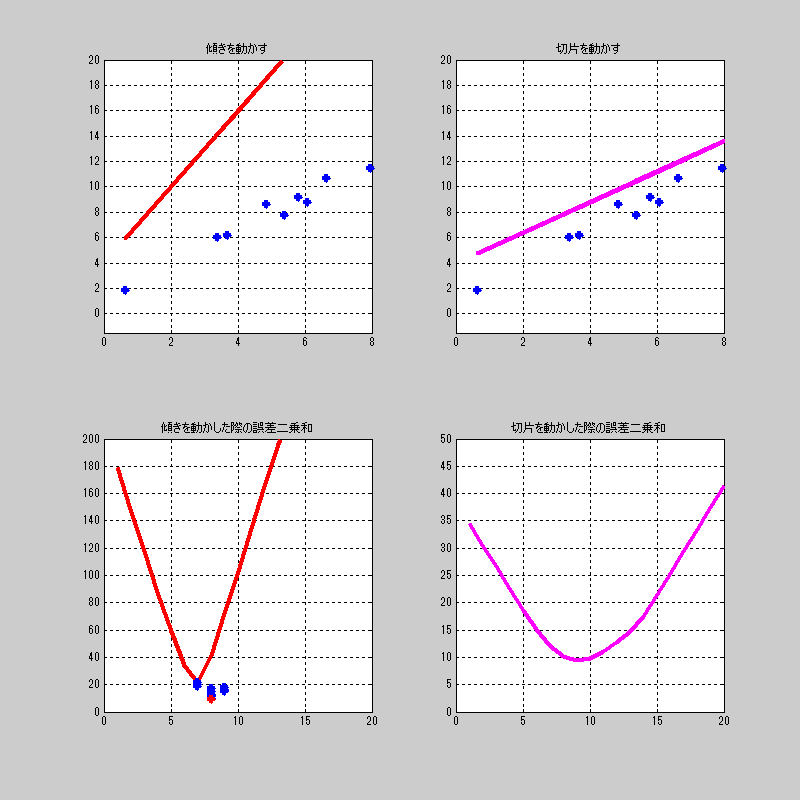

これも、おもしろい動きするね。

ちなみに、右下の傾きの誤差の最小値に対してプロットするようにしている。
全体を通して、最小値になるプロットだけを赤くしている。

つまり、完全に総当たりを行った後の赤いプロットが求めたい\((a,b)\)がわかるってことか。

でも、これって結構時間かからない?
あと、\(a\)と\(b\)をちょっとずつ動かしているといっても、その「ちょっと」って適正な値なのかな?

中々鋭いね。
太郎くんの危惧するように、総当たりの場合、時間の問題、精度の問題がネックになり、現実的な手法とは言い難い。

じゃーどうるすの?!!!

偏微分を使う。

は?

へ・ん・び・ぶ・ん

なんか偏頭痛がしてきた・・・。

偏微分は、別に複雑なものじゃないよ。
言葉の響きが「変な微分」って聞こえるからアレルギー反応をしめしちゃうのかもしれないけど、
どちらかというと、複雑で難しいものを簡単にするためのテクニックだな。
まぁ確かにその性質から、「複雑で難しいもの」を対象とするから、その印象で難しいものと認識しちゃうかもね。

とりあえず、解説はしてくれるんだよね・・・?

まぁ必要最低限の解説はするよ。

それを期待するか・・・。
まとめ

まとめだよ。
- 誤差関数の最小値を求める方法として総当たりがある。
- しかし、時間がかかったり、精度の設定の適切性が問えないなどの問題があり現実的な手法とは言い難い。
- 誤差関数の最小値を求めるには偏微分を使用するのが王道。
- 偏微分は「変な微分」ではない。
- 偏微分自体は複雑なものではなく、複雑なものをシンプルに扱うためのもの。
バックナンバーはこちら。




コメント