MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 その71【状態空間モデル㉙】
を書き直したもの。
DCモータ状態空間モデルをJuliaでシミュレーションする。
DCモータ状態空間モデル
以下の状態空間モデルをJuliaでシミュレーションする。
状態方程式
\(
\begin{bmatrix}
\dot{\theta}(t) \\
\dot{\omega}(t) \\
\dot{I}(t)
\end{bmatrix}=
\begin{bmatrix}
0 && 1 && 0 \\
0 && 0 && K/J \\
0 && -K/L && -R/L
\end{bmatrix}
\begin{bmatrix}
\theta(t) \\
\omega(t) \\
I(t)
\end{bmatrix}+
\begin{bmatrix}
0 \\
0 \\
1/L
\end{bmatrix}
E(t)
\)
出力方程式
\(
\boldsymbol{y}=
\begin{bmatrix}
1 && 0 && 0 \\
0 && 1 && 0 \\
0 && 0 && 1 \\
\end{bmatrix}
\begin{bmatrix}
\theta(t) \\
\omega(t) \\
I(t)
\end{bmatrix}+
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
E(t)
\)
Juliaコード
以下がJuliaによるシミュレーションコード。
using PyPlot
function statespacemodel(A,B,C,D,u,dt,x)
# 状態方程式
x = x + (A*x + B*u) * dt;
# 出力方程式
y = C*x + D*u;
return x,y;
end
function statespacemodel_motor()
K=0.016;
J=0.000000919;
R=1.34;
L=0.00012;
A=[0 1 0 ; 0 0 K/J ; 0 -K/L -R/L];
B=[0 ; 0; 1/L];
C=[1.0 0 0; 0 1.0 0; 0 0 1.0];
D=[0.0 ; 0.0 ; 0.0];
dt = 0.0001;
t = range(0, 10-dt, step=dt); # 時間(横)軸
u = zeros(1,100000); # 入力信号生成
u[1,50000:100000].=1.0; # 5秒後に0から1へ
y = zeros(3,length(t));
x = zeros(3,1);
for i = 1:length(t)
x,y[:,i] = statespacemodel(A,B,C,D,reshape(u[:,i],1,1),dt,x);
end
subplot(3,1,1);
plot(t,u[1,:]);
ylim([-0.05,1.1]);
xlim([4.95,5.25]);
subplot(3,1,2);
plot(t,y[1:2,:]');
ylim([-0.05,80]);
xlim([4.95,5.25]);
subplot(3,1,3);
plot(t,y[3,:]);
xlim([4.95,5.25]);
return y;
end
statespacemodel_motor();予想通りではあるけど、かなりMATLABに似ている。
差は、linspaceがrangeになってるくらい。
シミュレーション結果
シミュレーション結果は以下となる。
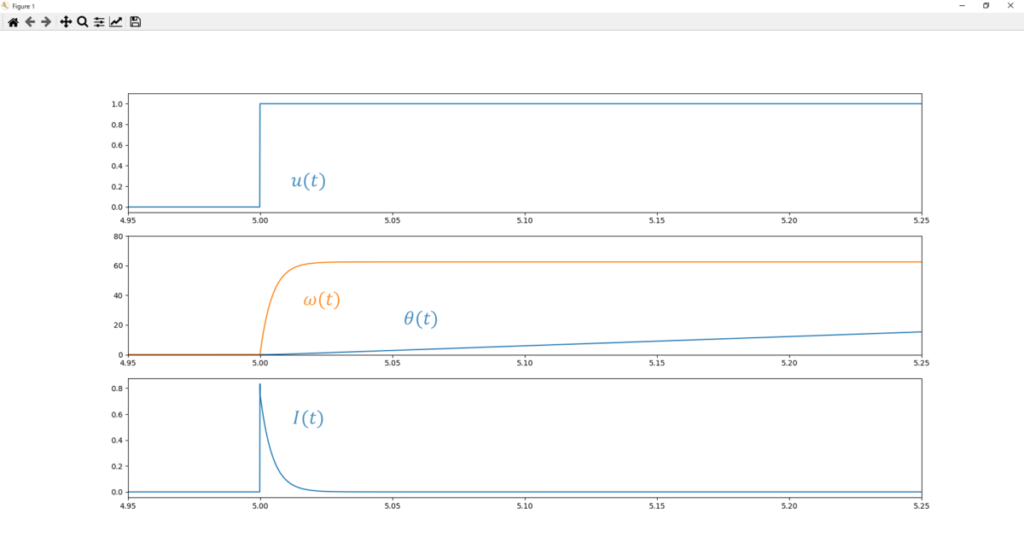
これも想定通りの振る舞い。
まとめ
- DCモータ状態空間モデルをJuliaでシミュレーション。
- かなりMATLABと近似のコードになる。
- linspaceがrangeになってるくらい。
- シミュレーションも同一であり、想定通り。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント