バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回は、Python(Numpy)によるDCモータ状態空間モデルのシミュレーションを実施。
今回は、これのScilab版
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】DCモータ状態空間モデル

流れ的にはScilabでDCモータ状態空間モデルシミュレーションの回になるね。

まずは、恒例のDCモータ状態空間モデルの再掲だ。
状態方程式
\(
\begin{bmatrix}
\dot{\theta}(t) \\
\dot{\omega}(t) \\
\dot{I}(t)
\end{bmatrix}=
\begin{bmatrix}
0 && 1 && 0 \\
0 && 0 && K/J \\
0 && -K/L && -R/L
\end{bmatrix}
\begin{bmatrix}
\theta(t) \\
\omega(t) \\
I(t)
\end{bmatrix}+
\begin{bmatrix}
0 \\
0 \\
1/L
\end{bmatrix}
E(t)
\)
出力方程式
\(
\boldsymbol{y}=
\begin{bmatrix}
1 && 0 && 0 \\
0 && 1 && 0 \\
0 && 0 && 1 \\
\end{bmatrix}
\begin{bmatrix}
\theta(t) \\
\omega(t) \\
I(t)
\end{bmatrix}+
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
E(t)
\)
Scilabコード

Scilabコードは以下になる。
function [x,y] = statespacemodel(A, B, C, D, u, dt, x)
% 様態方程式
x = x + (A*x + B*u) * dt;
% 出力方程式
y = C*x + D*u;
end
K=0.016;
J=0.000000919;
R=1.34;
L=0.00012;
A=[0,1,0 ; 0,0,K/J ; 0,-K/L,-R/L];
B=[0 ; 0; 1/L];
C=[1,0,0;0,1,0;0,0,1];
D=[0;0;0];
dt = 0.0001;
t = linspace(0, 10, 100000); // 時間(横)軸
u = zeros(1,100000); // 入力信号生成
u(1,50000:100000)=1; // 5秒後に0から1へ
y = zeros(3,length(t));
x = zeros(3,1);
for i = 1:length(t)
[x,y(:,i)] = statespacemodel(A,B,C,D,u(:,i),dt,x);
end
subplot(3,1,1);
plot(t,u);
p=gca();
p.tight_limits(:)="on"
p.data_bounds(:,2)=[-0.05;1.1];
p.data_bounds(:,1)=[4.95;5.25];
subplot(3,1,2);
plot(t,y(1:2,:));
p=gca();
p.tight_limits(:)="on"
p.data_bounds(:,2)=[-1;80];
p.data_bounds(:,1)=[4.95;5.25];
subplot(3,1,3);
plot(t,y(3,:));
p=gca();
p.tight_limits(:)="on"
p.data_bounds(:,1)=[4.95;5.25];
演算部分に関してはMATLABと同一だね。
グラフ表示の微調整の仕方がクセ違うけど。

そうだね。
グラフ表示もMATLABに合わせてくれると楽なんだけど、まぁそれほど問題になることもないだろう。
シミュレーション

シミュレーション結果は以下となる。
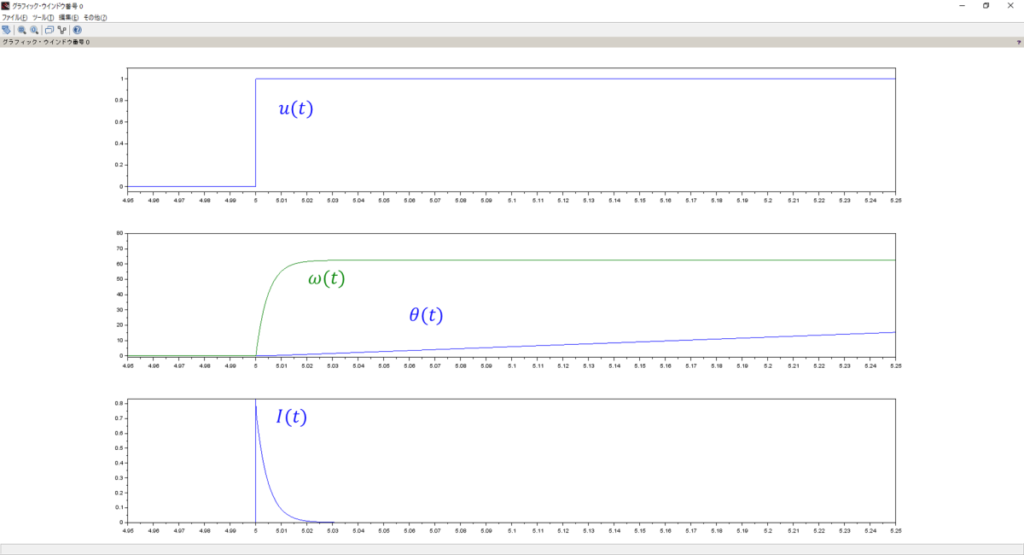

これも同じ結果と言えるね。

まぁ演算自体は全く一緒だもんね。
まとめ

まとめだよ。
- DCモータ状態空間モデルをScilabでシミュレーション。
- 演算自体はMATLABと同一。
- 差はグラフ表示の微調整のところ。
- シミュレーションも同一であり、想定通り。
バックナンバーはこちら。




コメント