MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 その61【状態空間モデル⑲】
を書き直したもの。
ニュートンの運動方程式を状態空間モデルを離散化したものをJuliaでシミュレーションする。
微分解決済みの状態空間モデル
以下がニュートンの運動方程式を状態空間モデルを離散化したもの。
これをJuliaで表現する。
状態方程式
\(\boldsymbol{x}(t+\Delta t)=\boldsymbol{x}(t)+\{A\boldsymbol{x}(t)+B\boldsymbol{u}(t)\}\Delta t \)
出力方程式
\(\boldsymbol{y}(t+\Delta t)=C\boldsymbol{x}(t+\Delta t)+D\boldsymbol{u}(t)\)
Juliaコード
using PyPlot
function statespacemodel(A,B,C,D,u,dt,x)
# 状態方程式
x = x + (A*x + B*u) * dt;
# 出力方程式
y = C*x + D*u;
return x,y;
end
function statespacemodel_test()
m=1;
A=[0 0; 1 0];
B=[1/m; 0];
C=[1 0; 0 1];
D=[0; 0];
dt=0.001;
t=range(0,10,length=10000); # 時間(横)軸
u=zeros(1,10000); # 入力信号生成
u[5000:10000].=1.0; # 5秒後に0から1へ
y=zeros(2,length(t));
x=zeros(2,1);
for i = 1:length(t)
x,y[:,i] = statespacemodel(A,B,C,D,u[i],dt,x);
end
plot(t',y');
plot(t',u', "--b");
grid();
end
statespacemodel_test()MATLABコードと全く一緒。
厳密差異としては以下がある。
配列の添え字が丸カッコか角カッコか。
ドット演算子を使用している。
u[5000:10000].=1.0ここまで差異が無いと、自宅での実験はJuliaでも良いかも?
シミュレーション結果
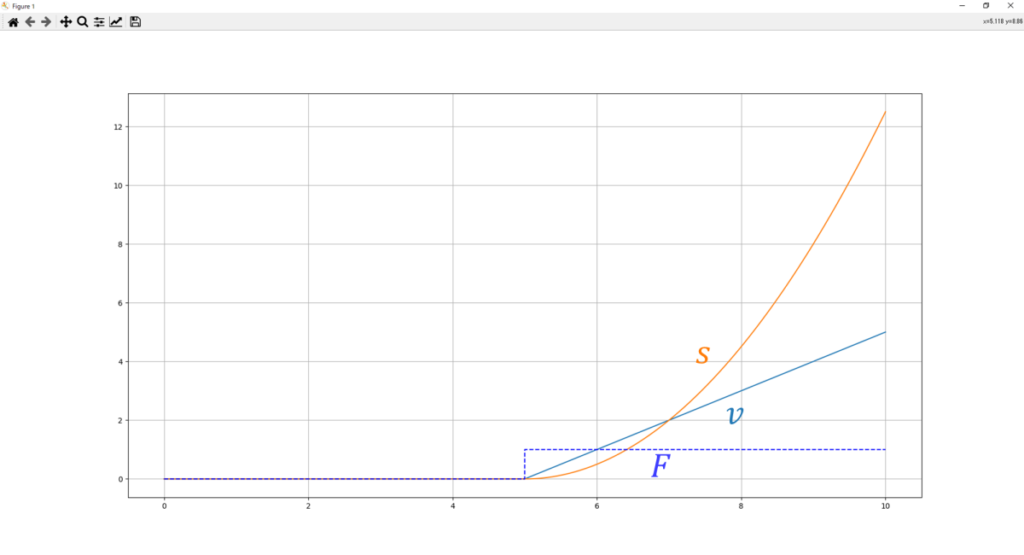
まとめ
- Juliaでベクトル、行列演算による状態空間モデルの演算実施。
- MATLABとほぼ同一。
- 添え字、ドット演算子に違いあり。
- シミュレーション結果も想定通り。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント