バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回までで、各ツール各言語による状態空間モデルのベクトル行列演算による実現をしたところ。
よくよく考えると、Cコード化という作業があるようなないような。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
Cコード化可能か?

ふと思ったんだけど?

何?

状態空間モデルを使用しない場合はCコード化までやったじゃん?
状態空間モデルを使用する場合Cコード化はどうなるの?

まぁベクトル行列演算用のライブラリを作ってやることもあるが、
C言語の場合、動的に配列を定義することが難しかったり、
オーバーヘッドがあったりする。
よって、想定される配列の大きさを決めてからCコード化することは多いな。

うーん、イメージがわかん。

じゃ、とりあえずMATLAB Coderで今回の状態空間モデルがどのようにCコードとして表現されるか見ているか。

自分で書かないのか?!

いや、結構メンドクサイから・・・。

まぁ、まずは微分解決済みの状態空間モデルの再掲しておこう。
状態方程式
\(\boldsymbol{x}(t+\Delta t)=\boldsymbol{x}(t)+\{A\boldsymbol{x}(t)+B\boldsymbol{u}(t)\}\Delta t \)
出力方程式
\(\boldsymbol{y}(t+\Delta T)=C\boldsymbol{x}(t+\Delta t)+D\boldsymbol{u}(t)\)
Cコード

以下がMATLAB Coderが出力したものにたいして、若干の修正を入れたものだ。
/*
* main.c
*
* Code generation for function 'main'
*
*/
/* Include files */
#include <stdio.h>
#include "rt_nonfinite.h"
#include "main.h"
/* Type Definitions */
/* Named Constants */
/* Variable Declarations */
/* Variable Definitions */
/* Function Declarations */
static void b_statespacemodel(const real_T A[4], const real_T B[2], const real_T
C[4], const real_T D[2], real_T u, real_T dt, real_T x[2], real_T y[2]);
static void eml_xgemm(const real_T A[4], const real_T B[2], real_T C[2]);
/* Function Definitions */
static void eml_xgemm(const real_T A[4], const real_T B[2], real_T C[2])
{
int32_T i1;
int32_T i2;
for (i1 = 0; i1 < 2; i1++) {
C[i1] = 0.0;
for (i2 = 0; i2 < 2; i2++) {
C[i1] += A[i1 + (i2 << 1)] * B[i2];
}
}
}
real_T y[20000];
void main()
{
statespacemodel_motion_raw(y);
}
void statespacemodel(const real_T A[4], const real_T B[2], const real_T C[4],
const real_T D[2], real_T u, real_T dt, real_T x[2], real_T
y[2])
{
real_T dv5[2];
int32_T i;
/* 様態方程式 */
for (i = 0; i < 2; i++) {
dv5[i] = 0.0;
}
eml_xgemm(A, x, dv5);
for (i = 0; i < 2; i++) {
x[i] += (dv5[i] + B[i] * u) * dt;
}
/* 出力方程式 */
for (i = 0; i < 2; i++) {
y[i] = 0.0;
}
eml_xgemm(C, x, y);
for (i = 0; i < 2; i++) {
y[i] += D[i] * u;
}
}
int8_T u[10000];
void statespacemodel_motion_raw()
{
real_T x[2];
int32_T i;
real_T dv0[2];
real_T dv1[2];
int32_T i0;
static const real_T dv2[4] = { 1.0, 0.0, 0.0, 1.0 };
static const real_T dv3[4] = { 0.0, 1.0, 0.0, 0.0 };
/* 時間(横)軸 */
memset(&u[0], 0, 10000U * sizeof(int8_T));
/* 入力信号生成 */
memset(&u[4999], 1, 5001U * sizeof(int8_T));
/* 5秒後に0から1へ */
memset(&y[0], 0, 20000U * sizeof(real_T));
for (i = 0; i < 2; i++) {
x[i] = 0.0;
}
printf("F,v,s\n");
for (i = 0; i < 10000; i++) {
for (i0 = 0; i0 < 2; i0++) {
dv0[i0] = 1.0 - (real_T)i0;
dv1[i0] = 0.0;
}
statespacemodel(dv3, dv0, dv2, dv1, (real_T)u[i], 0.001, x, *(real_T (*)[2])
&y[i << 1]);
printf("%d,%lf,%lf\n",u[i], x[0], x[1]);
}
}
/* End of code generation (main.c) */
修正ってなにしたの?

ローカル変数に巨大な配列が定義されてしまうので、
それをグローバル変数に移動させた。
以下が該当する。
real_T y[20000];
int8_T u[10000];
あ、なるほど。
スタックオーバーフローしちゃうのね。

あとは挙動を確認できるようにprintfを追加した。

それは以前もやってたねー。
シミュレーション結果

そしてシミュレーション結果。
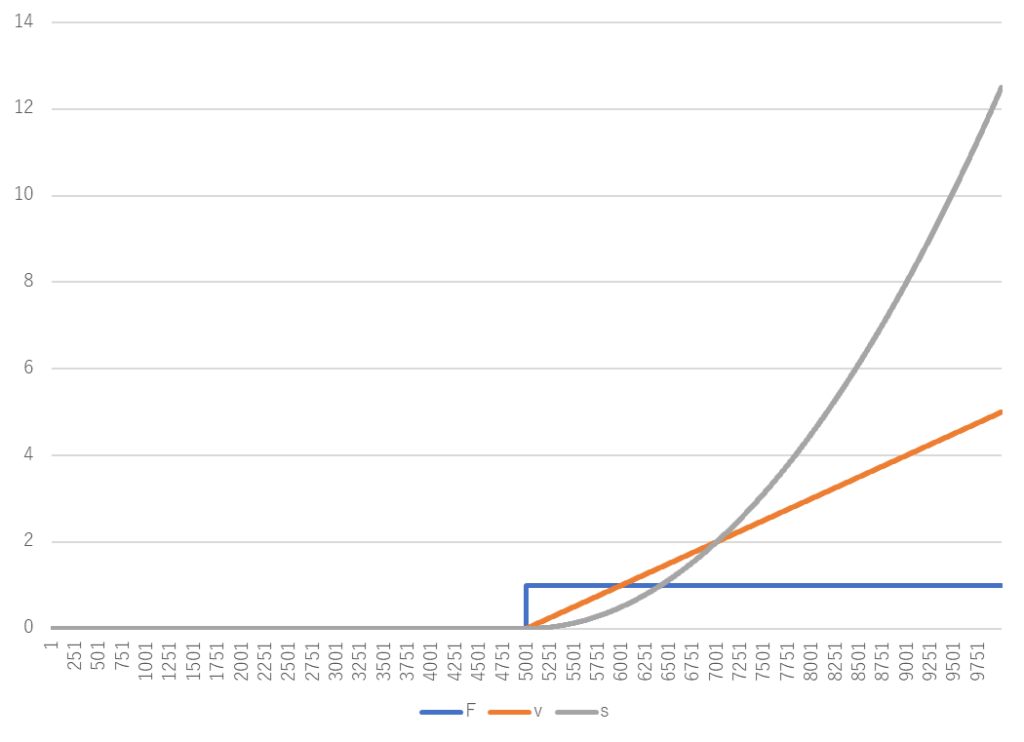

おー、ちゃんと同じ動きしてるねー!

まぁMATLAB Coderから出力したしね。

しかし、Cコードとしては結構ややこしいことになるんだな。

そうだね。
といっても、多変量になった場合は、一個一個の微分方程式を管理する方が面倒なこともあるからな。

扱う微分方程式が増えてきたら効果が大きくなるってことか。
まとめ

まとめだよ。
- Cコードによるベクトル、行列演算による状態空間モデルの演算実施。
- MATLAB Coderで出力。
- シミュレーション結果も想定通り。
- コード自体は複雑になるが、多変量の微分方程式になった際に効果は大きくなる。
バックナンバーはこちら。



コメント