バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回は状態空間モデルの演算をベクトル行列で行ったものをScilabで実施。
今回は、これのJulia版
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】微分解決済みの状態空間モデル

まずは、微分解決済みの状態空間モデルの再掲。
状態方程式
\(\boldsymbol{x}(t+\Delta t)=\boldsymbol{x}(t)+\{A\boldsymbol{x}(t)+B\boldsymbol{u}(t)\}\Delta t \)
出力方程式
\(\boldsymbol{y}(t+\Delta T)=C\boldsymbol{x}(t+\Delta t)+D\boldsymbol{u}(t)\)

今回はJuliaになると思うのだけど、
大体MATLABと一緒なのかな?

結果的にはそうだね。
まぁコードを見てみよう。
Juliaコード
using PyPlot
function statespacemodel(A,B,C,D,u,dt,x)
# 状態方程式
x = x + (A*x + B*u) * dt;
# 出力方程式
y = C*x + D*u;
return x,y;
end
function statespacemodel_test()
m=1;
A=[0 0; 1 0];
B=[1/m; 0];
C=[1 0; 0 1];
D=[0; 0];
dt=0.001;
t=range(0,10,length=10000); # 時間(横)軸
u=zeros(1,10000); # 入力信号生成
u[5000:10000].=1.0; # 5秒後に0から1へ
y=zeros(2,length(t));
x=zeros(2,1);
for i = 1:length(t)
x,y[:,i] = statespacemodel(A,B,C,D,u[i],dt,x);
end
plot(t',y');
plot(t',u', "--b");
grid();
end
statespacemodel_test()
これはMATLABコードと全くいっしょか。

配列の添え字が丸カッコか角カッコか、
u[5000:10000].=1.0
の部分でドット演算子を使用している。
の違いだけだな。

ここまで似ているのはありがたいね。
シミュレーション結果

そしてシミュレーション結果。
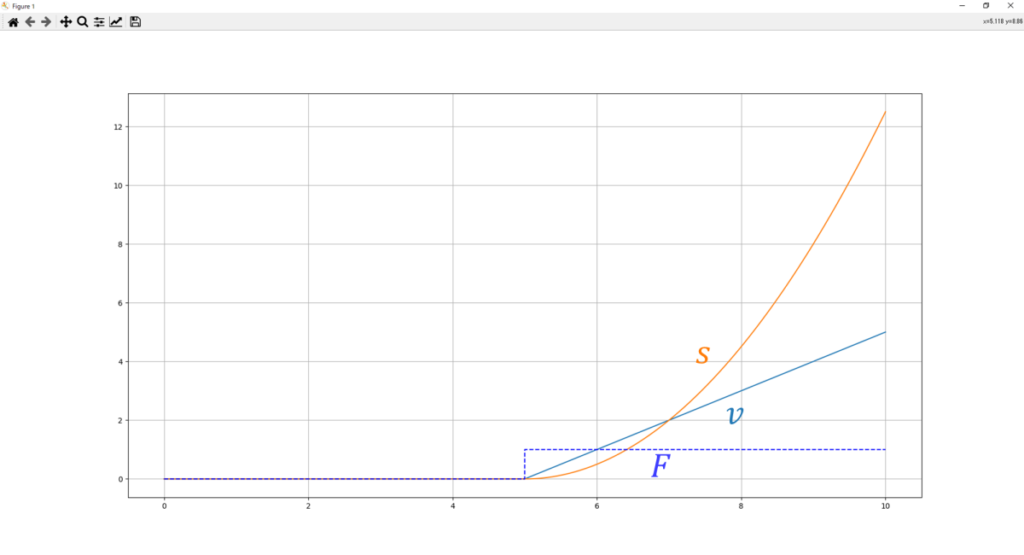

これも一緒だねー。

これは、自宅で実験する際はPython、ScilabじゃなくてJuliaってのもありなのか?

そうだね。
私もそういう使い方はアリな気がしてきたな。
まぁ若干独特な文化は感じるが、慣れれば問題無いと思う。
まとめ

まとめだよ。
- Juliaでベクトル、行列演算による状態空間モデルの演算実施。
- MATLABとほぼ同一。
- 添え字、ドット演算子に違いあり。
- シミュレーション結果も想定通り。
バックナンバーはこちら。




コメント