バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回から、状態空間モデルの掘り下げの話に突入。
まずは状態空間モデルを使用しないパターンをやってみる。
漸化式は前回出したので、ブロック図、C言語化にチャレンジ。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
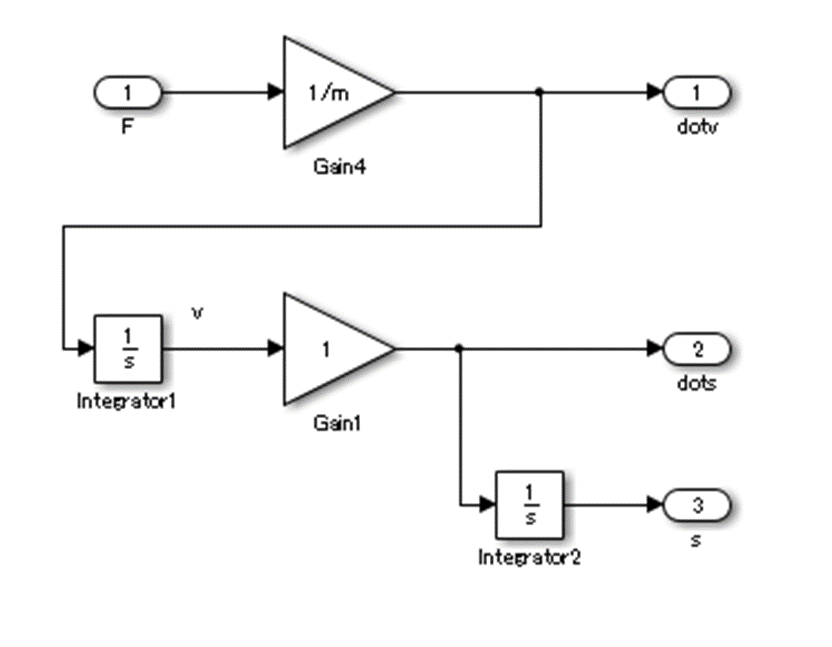
運動方程式のブロック図

じゃ、運動方程式のブロック図をざっと書いておこう。
ちなみにガチで書くとメンドサイからSimulinkで書いた。

Simulinkで書いたなら、もうこれでシミュレーションとオートコード生成しちゃえばいいじゃんって思うな・・・。

まぁそれが現行のプロセスではあるけど、
そこは一個ずつ手作業でやるって体で進める。
じゃないと一瞬で終わって状態空間モデルの利点が伝わらない。

とすると、現状だと状態空間モデルの利点がないってことになるんじゃ・・・。

そこはまぁ一通りやってみてから再度考察しよう。
運動方程式のブロック図の離散化

先のブロック図は連続系。
これを離散化する必要がある。
まぁ積分器のところを加算器にさしかえるだけなんだけど。
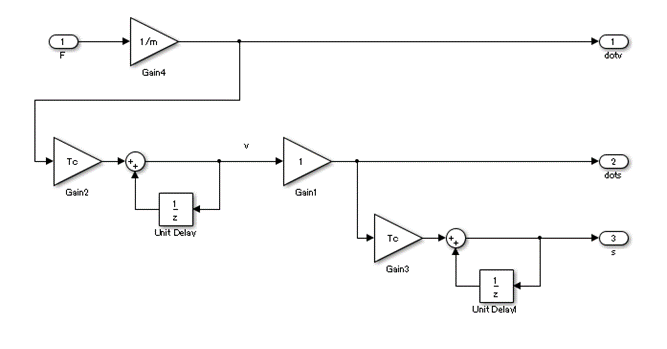

これも良く見かけるな。
オートコード生成する場合はこれからやる感じかな。
再度漸化式

そして、前回すでに書きだしたが、
この離散化したブロック図を元に漸化式を導出する。
速度の漸化式
\(\boldsymbol{\dot{v}}(t)=\displaystyle \frac{1}{m}\boldsymbol{F}(t)\)
\(\boldsymbol{v}(t)=\boldsymbol{\dot{v}}(t)\Delta T + \boldsymbol{v}(t-\Delta T) \)
距離の漸化式
\(\boldsymbol{\dot{s}}(t)=\boldsymbol{v}(t)\)
\(\boldsymbol{s}(t)=\boldsymbol{\dot{s}}(t)\Delta T + \boldsymbol{s}(t-\Delta T) \)

なるほど。
離散化したブロック図があれば、この漸化式もそのまんま数式にしているだけってのはわかるな。

そして漸化式があると、Cコード化が可能になる。

え?可能なの?
オートコードが出せるのは分かるけど、
手作業でCコード化はイメージ湧かないなぁ。

企業によっては漸化式からフローチャートにして、
そこからCコード化ってプロセスを踏んでるところもあるようだな。

ちょっと、どんな感じのコードになるか見たいんだけど・・・。

じゃ、次回までにCコードを起こしておこう。
まとめ

まとめだよ。
- 運動方程式をブロック図で書き起こした。
- エディタの利便性からSimulinkを利用。
- 上記を離散化。
- Simulink利用の場合、この段階からオートコード生成。
- 離散化ブロックを元に漸化式。
- これからCコード化をする。(次回Cコードを見せる予定)
バックナンバーはこちら。




コメント