G検定記事はこちら。
https://www.simulationroom999.com/blog/jdla-deep-learning-for-general-2020-1/
はじめに
AIはボードゲームでも利用される。
(オセロ、チェス、将棋、囲碁など)
これらの実現手段の概要を記載する。
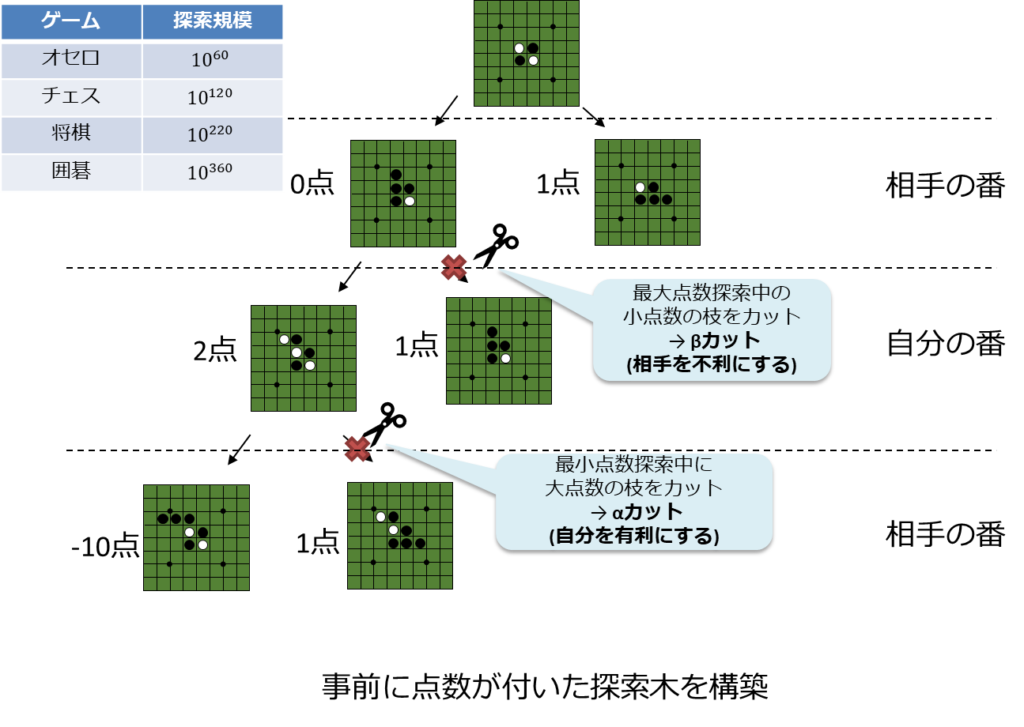
ボードゲームの探索規模
これも基本は探索木になる。
迷路の探索木に似ているが、「行動」と「結果」の連続した探索木となるが、局面が複雑化するタイプになると、それだけ膨大なツリーとなる。
探索木の規模は以下となる。
| オセロ | $${10^{60}}$$ |
| チェス | $${10^{120}}$$ |
| 将棋 | $$10^{220}$$ |
| 囲碁 | $$10^{360}$$ |
ヒューリスティックな知識
単純な総当たりな探索では時間が掛かるため、ゴールまでのコストという概念を用いて、
最適化を行う必要が出てくる。
これを「ヒューリスティックな知識」と言う。
Mini-Max法
上記のコストを点数として考え、以下の状態を優先的に狙う手法
- 相手を不利(最小点数)
- 自分を有利(最大点数)
完全情報零和ゲームに向いているとされている。
完全情報零和ゲームとは、すべての情報が開示されており、次のゲームに前のゲームの結果が影響しないものである。
Mini-Max法で探索木を縮小させる手法が存在しており、それをαβ法と呼ぶ。
- 最小点数探索中に大点数の枝をカット → αカット
- 最大点数探索中の小点数の枝をカット → βカット
まとめ
- すべての結果が分かれば確実に勝てるという考え方。
- しかし、相当な計算能力が必要とされる。
- オセロ < チェス < 将棋 < 囲碁
- 計算能力を削減するためにMini-Max法、αβ法が考え出された。




コメント